什么是公差累积?为什么它很重要?
统计公差分析是指利用一组输入变量的变化来计算感兴趣的输出变量的预期变化。在机械工程中,产品设计由多个特征组成,每个特征都有控制这些特征变化方面的公差值。统计公差分析用于理解这些公差是如何影响设计的各种性能特征的。

公差累积分析是机械设计中的关键步骤,它帮助我们理解各个零件的公差是如何共同影响整个装配的性能。这种分析对于确保机械装配的精确性和机械部件的性能至关重要。简单来说,公差累积分析回答了这样一个问题:“组成装配的各个零件是否能够始终正确地组装在一起?”此外,它还涵盖了机械性能的要求,比如开关、扣件、执行器等部件的功能,以及光学对准或电机效率等其他性能指标。“累积”在这里指的是将各个零件的公差叠加起来,以评估它们对整体设计的影响。
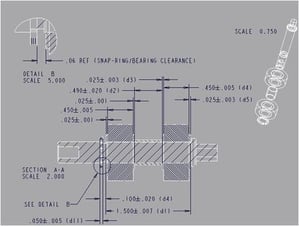
在进行公差累积分析时,我们会计算零件公差的累积效应,并将其与装配要求的间隙或性能限制进行比较,以验证设计是否可行。这种方法也被称为最坏情况分析,适用于那些一旦失败可能会给公司带来灾难性后果的应用场景,或者涉及少量零件的情况。最坏情况分析通常是单向的,即1D分析。如果分析的零件尺寸与装配测量的方向不平行,那么就需要调整累积方法,因为2D变化(例如角度)或任何不与1D方向平行的变化,不会直接以1:1的比例影响装配测量。
许多公司采用统计公差分析方法,其中一种常用的方法是RSS(Root-Sum-Squared),即根和平方和方法。与最坏情况分析直接相加公差不同,统计分析将尺寸分布相加。最坏情况分析使用的是设计公差作为输入值,而统计分析则使用过程分布矩(例如标准差)作为输入。最坏情况分析可以用来验证设计,而统计分析则可以预测基于零件尺寸变化的装配的实际变化。通过比较装配的标准差和装配限制,我们可以计算出如西格玛、产量百分比、DPMU等质量指标。这种方法要求所有零件的分布都是正态的,并且质量水平一致,即±3σ。

对于RSS方法的局限性,已经开发出了其他计算装配变异的方法。CETOL 6 Sigma中采用的系统矩法就是其中之一,它克服了RSS的局限。现在,无论是1D、2D还是3D的分析,都可以不受分布类型或质量水平限制地进行。这使得公司能够使用公差分析软件进行全面的装配变异分析。
装配变异分析提供了必要的洞察,帮助我们识别出必须控制的关键零件特性(KPCs),以生产出满足客户期望的产品。产品开发过程应专注于定义和验证能够实现高生产水平的零件制造和装配过程。常见的目标是关键特征的Cpk达到1.67,非关键特征的Cp达到1.33。利用变异分析的洞察,设计工程师可以战略性地分配公差预算,对关键特征实施更严格的公差控制,而对较不重要的特征则可以采用更宽松的公差。这些决策不仅确保了产品的质量和性能,还确保了产品的可制造性,并且能够在合理的成本下生产。这种分析对产品开发过程的影响是巨大的。